There are several ways in which the two sets S and T may be related:
Suppose we have two sets, S and T. A relation on S and T is a set of ordered pairs, where the first thing in each pair is an element of S, and the second thing is an element of T.
For example, suppose S is the set {A, B, C, D, E}, while T is the set {W, X, Y, Z}. Then one relation on S and T is {(A,Y), (C,W), (C,Z), (D,Y)}. There are four ordered pairs in the relation. We can draw this as four arrows going from S to T (see Figure 2). One arrow goes from A to Y; another goes from C to W; another goes from C to Z; and another goes from D to Y.
The purpose of this page is just to define terms. Giving names to things is not important unless you can later use those names to talk about the things. These terms we define here are used throughout mathematics, and are pretty important; but we don't go into any of that here. We just define the terms.
The most important of the terms we will define is function. You have probably seen this word defined in algebra or calculus, and you may think this is another meaning for the same word. It's important to realize that there is only one meaning in mathematics for the word "function", and this is it. Moreover, the definition given here is the "best" definition because, since the definition is given in terms of sets, it is the most general and most applicable definition. Any other definition is just a special case.
Anyway, to continue.
The domain of a relation on S and T is the set of elements of S that appear as the first element in an ordered pair of the relation. In the relation {(A,Y), (C,W), (C,Z), (D,Y)}, the domain is {A, C, D}. If you look at Figure 2, these are the elements of S that have arrows coming out of them.
The range of a relation on S and T is the set of elements of T that appear as the second element in an ordered pair of the relation. In the relation {(A,Y), (C,W), (C,Z), (D,Y)}, the range is {W, Y, Z}. If you look at Figure 2, these are the elements of T that have arrows pointing to them.
For some reason, the word codomain has become popular as a synonym for "range." I think it's an ugly word. If anyone has an explanation for why this word has become popular, I would very much like to hear it.
In Figure 2, not every element of T has an arrow pointing to it. That is, there are some elements of T (in particular, the element X) that do not occur as a second element of an ordered pair. We say that the relation is into T.
Suppose we have a relation in which every element occurs (at least once) as a second element of an ordered pair. For example, the relation {(A,Y), (B, X), (C,W), (C,Z), (D,Y)} (See Figure 3) is just like the previous relation, except that it also contains the ordered pair (B, X). The relation is onto: every element of set T has an arrow (at least one) pointing to it.
While the word "onto" has a precise definition (the range of the relation is the set T itself), the word "into" is not usually so well defined. "Into" could be used to mean "not onto" (there is at least one element of T that does not have an arrow pointing to it), or it could mean "not necessarily onto", that is, there might be some element of T that does not have an arrow pointing to it. Different authors might choose to define "into" in different ways, or not define it precisely, or just not define it at all.
Suppose we put in every possible arrow from S to T. That is, from each element of S we draw arrows to each element of T (see Figure 4). This "largest possible relation" is called the Cartesian product of S and T. Every other relation on S and T is a subset of the Cartesian product.
(How is it possible for a relation to be a subset of another relation? Remember that a relation is just a set of ordered pairs. Or, in our pictures, a relation is a set of arrows.)
Next we will say that a relation is one to one, or 1-1, if no element of S occurs more than once as the first element of an ordered pair, and no element of T occurs more than once as a second element of an ordered pair. In other words, no element of S or T has more than a single arrow attached to it. (See Figure 5).
(This definition holds even when S and T are not disjoint, but the picture is a little more confusing. An element that is in both S and T could have a single arrow attached to it, as before, but at both ends!)
Another word for function is mapping.
A function is said to map an element in its domain
to an element in its range.
Here are some important facts about a function from S to T:
To tell whether a relation on S and T is a function,
you can ignore T altogether.
Just look at S.
If every element of S has one and only one element
coming out of it,
then the relation is a function.
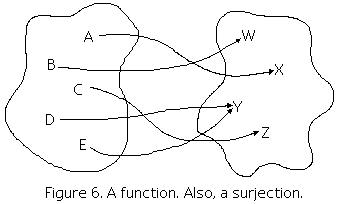
A surjection or onto function from S to T
is a function whose range is T itself.
That is, every element of T has at least one arrow pointing to it;
so the relation is onto.
Figure 6 is an example of a surjection.
Since the domain of a function from S to T is the
entire set S (by the definition of function),
and since the range of a surjective function from S to T
is the entire set T, this means that every element of
both sets is in the relation (has an arrow connected to it).
Also note that if you have a surjection from S to T,
S may have more elements than T,
or it may have the same number of elements,
but it cannot have fewer elements than T.
This is because every element of S has exactly one arrow
emanating from it,
but each element of T has at least one arrow
pointing to it, and could have many.
An injection or one-to-one function from S to T
is a function that is one to one.
That is, every element in both S and T has at least one arrow
attached to it.
By the definition of function, of course, every element of S
has exactly one arrow emanating from it, no more, no less.
A one-to-one function also requires that every element of
T can have no more than one arrow pointing to it;
but there could be elements of T that do not have any
arrows pointing to them.
Figure 7 shows an injection.
However, we had to modify the sets a little bit to get this example.
A little thought will show that, with an injection from S to T,
T must have at least as many elements as S.
To get our example, we removed some elements from S.
(We could equally as well have added elements to T.)
Finally, a function that is both 1-1 and onto is called a bijection.
Such a function maps each and every element of S
to exactly one element of T,
with no elements left over.
shows a bijection.
Again, we had to modify the sets a little because,
with a bijection,
sets S and T have to have exactly the same number of elements.
A bijection is particularly interesting because this kind of function
has an inverse.
If you took a bijection from S to T and reversed the direction
of all the arrows,
you would have a bijection from T to S.
This new function would be the inverse of the original function.
Kinds of functions
There are three kinds of functions that are
important enough to have special names:
surjection, injection, and bijection.
Back to Dave's home page.